Understand with an example
Before we jump into the core topic let’s discuss one example. We have a circular disc of radius as shown in the figure below.

There is a point p on the circumference of the disc and the question is how the path traced out by point p looks as the disc rolls forward.
If we draw the trajectory traced out by the point p, when the disc moves forward It looks something like this as shown in figure below. This trajectory is called a cycloid.
When the above curve is turned upside down the cycloid becomes a brachistrone or the shortest-time curve.

This curve has following two important properties:
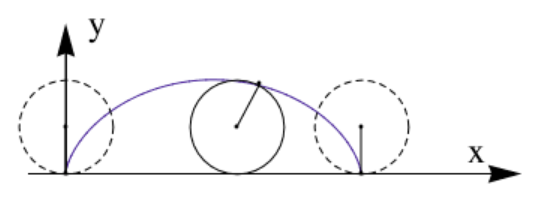
- The path which an object takes to go from point 'A' to 'B' in the shortest time possible under the influence of gravity is this brachistrone curve called a cycloid. So if the fall follows the brachistrone path then the fall time is the least of all possible paths.
- If the object starts to fall a little bit below the point 'A', say from point 'B' and the fall time is the same as that of fall time from point 'A'. Then the cycloid becomes a tautochrone or **same-time curve**.
Are there any other brachistochrones joining O and B, or is the cycloid the only one? We can formulate this as a mathematical question by making use of the work energy theorem.
The work energy theorem says “the work done by all forces acting on a particle equals the change in the particle’s kinetic energy”.
Let’s apply this theorem:
At the start, the kinetic energy of the bead is zero, since its velocity (speed) is zero. The work done by gravity in moving the bead from (0,0) to any other point (x,y) in the plane is mgy, and this must equal the change in kinetic energy.
\[mgy = \frac{1}{2}mv^2 - \frac{1}{2}m0^2\] \[mgy = \frac{1}{2}mv^2\]From the last equation we can express speed as a function of \(y\) after cancelling \(m\) from both sides. \(v=\sqrt{2gy}\) Now the speed \(v\) can be expressed as a time derivative of the distance \(S\). That is \(v=\frac{dS}{dT}\). Hence the differential time \(dT\) taken to cover infinitesimal distance \(dS\) is given by:
\[dT = \frac{dS}{V}\] \[Or\] \[dT = \frac{dS}{\sqrt{2gy}}\]It is well known that infinitesimal distance \(dS\) can be expressed in terms of \(dx\) and \(dy\) using pythagorean theorem. Therefore \(dS=\sqrt{dx^2+dy^2}\), when \(dx^2\) is factored out we have:
\[dS = dx\sqrt{1 + \frac{dy}{dx}}\]The equation for \(dT\) reduces to the following:
\[dT = \frac{dx\sqrt{1 + (\frac{dy}{dx})}}{\sqrt{2gy}}\]When distance traced is longer the time taken is given by integration of \(dT\). Therefore the time taken to move from one point of the curve to another, say from \(A\) to \(B\) is given by:
\[T = \int_{x=A}^{x=B} dx\sqrt{\frac{1 + (\frac{dy}{dx})}{2gy}}\]What curves \(y = ƒ(x)\), if any, minimize the value of this integral?
Ans: The branch of mathematics that deals with this problem is called calculus of variations. For this particular problem the equation of is that of a cycloid and it is the one and only brachistrone for point A and B.