Perturbation theory is a powerful tool in quantum mechanics used to study systems where the Hamiltonian can be separated into a known part $H_0$ and a small perturbation $H'$. The goal is to find approximate solutions to the Schrödinger equation for the full Hamiltonian $H = H_0 + H'$ by treating the perturbation as a small correction to the known system.

Time Independent Perturbation Theory: Non-degenerate Case

Suppose we have a Hamiltonian

\[H = H_0 + \lambda H'\]

where $\lambda$ is a small parameter. The Hamiltonian $H_0$ is the unperturbed Hamiltonian whose eigenvalues and eigenfunctions are known say $E_n^{(0)}$ and $\psi_n^{(0)}$ respectively. The Hamiltonian $H'$ is the perturbation to the Hamiltonian $H_0$. Now the problem is to find the eigenvalues and eigenfunctions of the Hamiltonian $H$.

If the unperturbed Hamiltonian $H_0$ is known, then the eigenvalues and eigenfunctions of $H$ can be found by using perturbation theory.
The eigenvalues and eigenfunctions of $H$ can be expanded in powers of $\lambda$.
The eigenvalues of $H$ are given by:
\[E_n = E_n^{(0)} + \lambda E_n^{(1)} + \lambda^2 E_n^{(2)} + \cdots\]
where $E_n^{(0)}$ are the eigenvalues of $H_0$ and $E_n^{(1)}$ are the first order corrections to the eigenvalues. Similarly, $E_n^{(2)}$ are the second order corrections to the eigenvalues.
The eigenfunctions of $H$ are given by:
\[\psi_n = \psi_n^{(0)} + \lambda \psi_n^{(1)} + \lambda^2 \psi_n^{(2)} + \cdots\]
where $\psi_n^{(0)}$ are the eigenfunctions of $H_0$ and $\psi_n^{(1)}$ are the first order corrections to the eigenfunctions. Similarly, $\psi_n^{(2)}$ are the second order corrections to the eigenfunctions.
The first order correction to the eigenvalues is given by:
\[E_n^{(1)} = \int \psi_n^{(0)*} H' \psi_n^{(0)} \, d\tau\]
One gets this by substituting the above expression for $E_n$ into the Schrödinger equation and then projecting the equation onto $\psi_n^{(0)}$. We will use the fact that
\[\int \psi_n^{(0)*} \psi_n \, d\tau = \int \psi_n^{(0)*} \psi_n^{(0)} \, d\tau = 1\]
Expanding the Schrödinger equation gives
\[\begin{align} \int \psi_n^{(0)*} (H_0 + \lambda H') \psi_n \, d\tau &= E_n \int \psi_n^{(0)*} \psi_n \, d\tau\\ \int \psi_n^{(0)*} H_0 \psi_n \, d\tau + \lambda \int \psi_n^{(0)*} H' \psi_n \, d\tau &= E_n \int \psi_n^{(0)*} \psi_n^{(0)} \, d\tau\\ E_n^{(0)} \int \psi_n^{(0)*} \psi_n \, d\tau + \lambda \int \psi_n^{(0)*} H' \psi_n \, d\tau &= E_n \\ E_n^{(0)} \int \psi_n^{(0)*} \psi_n^{(0)} \, d\tau + \lambda \int \psi_n^{(0)*} H' \psi_n \, d\tau &= E_n^{(0)}+ \lambda E_n^{(1)}+ \lambda^2 E_n^{(2)} + \cdots\\ E_n^{(0)}+ \lambda \int \psi_n^{(0)*} H' \psi_n \, d\tau &= E_n^{(0)}+ \lambda E_n^{(1)}+ \lambda^2 E_n^{(2)} + \cdots\\ \lambda \int \psi_n^{(0)*} H' \psi_n \, d\tau &= \lambda E_n^{(1)}+ \lambda^2 E_n^{(2)} + \cdots \end{align}\]
Expanding the perturbative term on L.H.S. of the above equation gives
\[\int \psi_n^{(0)*} H' \psi_n \, d\tau =\int \psi_n^{(0)*} H' \psi_n^{(0)} \, d\tau+ \lambda\int \psi_n^{(0)*} H' \psi_n^{(1)} \, d\tau+ \lambda^2\int \psi_n^{(0)*} H' \psi_n^{(2)} \, d\tau+ \cdots\]
therefore the Schrödinger equation gives

$\lambda\int \psi_n^{(0)*} H' \psi_n^{(0)} \, d\tau+ \lambda^2\int \psi_n^{(0)*} H' \psi_n^{(1)} \, d\tau+ \cdots=\lambda E_n^{(1)}+ \lambda^2 E_n^{(2)} + \cdots$

we get first order corrections to the eigenvalues as
\[\boxed{E_n^{(1)} = \int \psi_n^{(0)*} H' \psi_n^{(0)} \, d\tau}\]
First order correction can be calculated as the expression of the eigenfunction $\psi_n^{(0)}$ is well known and the matrix element of $H'$ can be calculated. The second order correction to the eigenvalues is given by:
\[\boxed{E_n^{(2)} = \int \psi_n^{(0)*} H' \psi_n^{(1)} \, d\tau}\]
Here the first order correction to the eigenfunction is needed to calculate the second order correction to the eigenvalues.
The first order correction to the eigenfunctions is given by:
\[\psi_n^{(1)} = \sum_{m \neq n} \frac{\int\psi_m^{(0)*} H' \psi_n^{(0)}d\tau}{E_n^{(0)} - E_m^{(0)}}\psi_m^{(0)}\]
The first order correction to the eigenfunction can be calculated by using the fact that the eigenfunctions of $H_0$ are known and the matrix elements of $H'$ can be calculated. The first order correction to the eigenfunction is calculated by projecting the Schrödinger equation onto the state $\psi_m^{(0)}$ where $m \neq n$.

Time Independent Perturbation Theory: Degenerate Case

In the degenerate case, we still have the Hamiltonian

\[H = H_0 + \lambda H'\]

where $\lambda$ is a small parameter. The unperturbed Hamiltonian $H_0$ has a set of degenerate eigenstates, meaning there are multiple eigenfunctions corresponding to the same eigenvalue $E_n^{(0)}$.

Problem Statement

The problem is to find the eigenvalues and eigenfunctions of the perturbed Hamiltonian $H$ when the unperturbed Hamiltonian $H_0$ has degenerate eigenstates.

Approach

For simplicity, assume that $H_0$ has a degenerate eigenvalue $E_n^{(0)}$ with $g$ degenerate states $\psi_{n,1}^{(0)}, \psi_{n,2}^{(0)}, \ldots, \psi_{n,g}^{(0)}$. We need to account for the mixing of these degenerate states due to the perturbation $H'$.

Eigenvalue and Eigenfunction Expansions

The eigenvalues and eigenfunctions of $H$ can still be expanded in powers of $\lambda$:

\[E_n = E_n^{(0)} + \lambda E_n^{(1)} + \lambda^2 E_n^{(2)} + \cdots\] \[\psi_n = \psi_n^{(0)} + \lambda \psi_n^{(1)} + \lambda^2 \psi_n^{(2)} + \cdots\]

However, now $\psi_n^{(0)}$ is a linear combination of the degenerate states:

\[\psi_n^{(0)} = \sum_{k=1}^{g} c_k \psi_{n,k}^{(0)}\]

First Order Correction to the Eigenvalues

To find the first order correction to the eigenvalues, we solve the secular equation by considering the matrix elements of $H'$ in the subspace of the degenerate states:

\[H'_{ij} = \langle \psi_{n,i}^{(0)} | H' | \psi_{n,j}^{(0)} \rangle\]

We need to solve the eigenvalue problem for the matrix $H'$ restricted to the degenerate subspace:

\[\sum_{j=1}^{g} H'_{ij} c_j = E_n^{(1)} c_i\]

This is equivalent to finding the eigenvalues and eigenvectors of the matrix $H'$ in the degenerate subspace. The eigenvalues of this matrix are the first order corrections $E_n^{(1)}$.

First Order Correction to the Eigenfunctions

Once the coefficients $c_i$ are found by solving the secular equation, the first order correction to the eigenfunction $\psi_n^{(0)}$ can be written as:

\[\psi_n^{(1)} = \sum_{m \neq n} \frac{\langle \psi_m^{(0)} | H' | \psi_n^{(0)} \rangle}{E_n^{(0)} - E_m^{(0)}} \psi_m^{(0)}\]

where $\psi_n^{(0)} = \sum_{k=1}^{g} c_k \psi_{n,k}^{(0)}$.

Summary

Solve the secular equation for the degenerate subspace:
\[\sum_{j=1}^{g} H'_{ij} c_j = E_n^{(1)} c_i\]
Find the first order correction to the eigenvalues by solving the eigenvalue problem for the matrix $H'$ in the degenerate subspace.
Compute the first order correction to the eigenfunctions using:
\[\psi_n^{(1)} = \sum_{m \neq n} \frac{\langle \psi_m^{(0)} | H' | \psi_n^{(0)} \rangle}{E_n^{(0)} - E_m^{(0)}} \psi_m^{(0)}\]
with $\psi_n^{(0)}$ expressed as a linear combination of the degenerate states.

Time-Dependent Perturbation Theory

Time-Dependent Perturbation Theory is an essential tool in quantum mechanics used to study systems under the influence of a time-varying external force or potential. It provides a way to calculate the probabilities of transitions between different quantum states over time.

Basic Concept

Consider a quantum system described by a time-independent Hamiltonian $\hat{H}_0$ with known eigenstates $ \ket{n} $ and corresponding energies $E_n$:

\[\hat{H}_0 \ket{n} = E_n \ket{n}\]

When a time-dependent perturbation $\hat{V}(t)$ is applied to the system, the total Hamiltonian becomes:

\[\hat{H}(t) = \hat{H}_0 + \hat{V}(t)\]

The perturbation $\hat{V}(t)$ is assumed to be small, so it induces transitions between the eigenstates of $\hat{H}_0$.

Perturbation Expansion

The state of the system $\ket{\Psi(t)}$ evolves according to the Schrödinger equation:

\[i\hbar \frac{\partial}{\partial t} \ket{\Psi(t)} = \hat{H}(t) \ket{\Psi(t)}\]

We express the state $\ket{\Psi(t)}$ as a superposition of the unperturbed eigenstates:

\[\ket{\Psi(t)}= \sum_n c_n(t) e^{-iE_n t/\hbar}\ket{n}\]

Here, $c_n(t)$ are the time-dependent coefficients that give the probability amplitude for the system to be in state $\ket{n}$ at time $t$.

First-Order Approximation

In the first-order approximation, the change in the coefficients $c_n(t)$ is given by:

\[c_n^{(1)}(t) = -\frac{i}{\hbar} \int_{t_0}^{t} \langle n|\hat{V}(t')|\Psi(t')\rangle e^{iE_n t'/\hbar} dt'\]

If the system starts in state $\ket{m}$ at $t_0$, we have:

\[c_n^{(1)}(t) = -\frac{i}{\hbar} \int_{t_0}^{t} \bra{n}\hat{V}(t')\ket{m} e^{i(E_n-E_m)t'/\hbar} dt'\]

This integral allows us to calculate the probability of the system transitioning from state $\ket{m}$ to state $\ket{n}$ due to the perturbation.

Transition Probability

The probability of the system being found in state $\ket{n}$ at time $t$ is given by $P_{m \to n}(t)$:

\[P_{m \to n}(t) = |c_n^{(1)}(t)|^2\]

For a sinusoidal perturbation of the form $\hat{V}(t) = \hat{V}_0 \cos(\omega t)$, this expression can be further simplified, leading to well-known results such as Fermi’s Golden Rule for transition rates.

Sudden Perturbation

In exploring time-dependent perturbation theory, we consider the case of fast or “sudden” perturbations. A perturbation is deemed sudden if the transition from one time-independent Hamiltonian $\hat{H}_0$ to another $\hat{H}'_0$ occurs over a time much shorter than any natural period of the system. In such cases, perturbation theory becomes irrelevant. If the system is initially in an eigenstate $\ket{n}$ of $\hat{H}_0$, its time evolution post-transition follows $\hat{H}'_0$. The initial state can then be expressed as a sum over the eigenstates of $\hat{H}'_0$:

\[\ket{n} = \sum_{n'} \ket{n'} \bra{n'} n \rangle\]

The key challenge is to ensure that the change is sudden enough, which is determined by estimating the actual time taken for the Hamiltonian to change and the periods of motion associated with the state $\ket{n}$ and its transitions to neighboring states.

Harmonic Perturbations: Fermi’s Golden Rule

Consider a system prepared in an initial state $\ket{i}$ that is perturbed by a periodic harmonic potential $V(t) = V e^{-i\omega t}$, which is abruptly switched on at $t = 0$. This scenario could represent an atom perturbed by an external oscillating electric field, like an incident light wave. We aim to determine the probability that at some later time $t$, the system is found in state $\ket{f}$.

From first-order perturbation theory, the coefficient $c^{(1)}_f(t)$ is given by:

\[c^{(1)}_f(t) = -\frac{i}{\hbar} \int_{0}^{t} dt' \bra{f} V \ket{i} e^{i(\omega_{fi} - \omega)t'} = -\frac{i}{\hbar} \bra{f} V \ket{i} \frac{e^{i(\omega_{fi} - \omega)t} - 1}{i(\omega_{fi} - \omega)}\]

The probability of the transition after time $t$ is then:

\[P_{i \to f}(t) = \left| c^{(1)}_f(t) \right|^2 = \frac{1}{\hbar^2} \left| \bra{f} V \ket{i} \right|^2 \left( \frac{\sin((\omega_{fi} - \omega)t/2)}{(\omega_{fi} - \omega)/2} \right)^2\]

By setting $\alpha = (\omega_{fi} - \omega)/2$, the probability becomes:

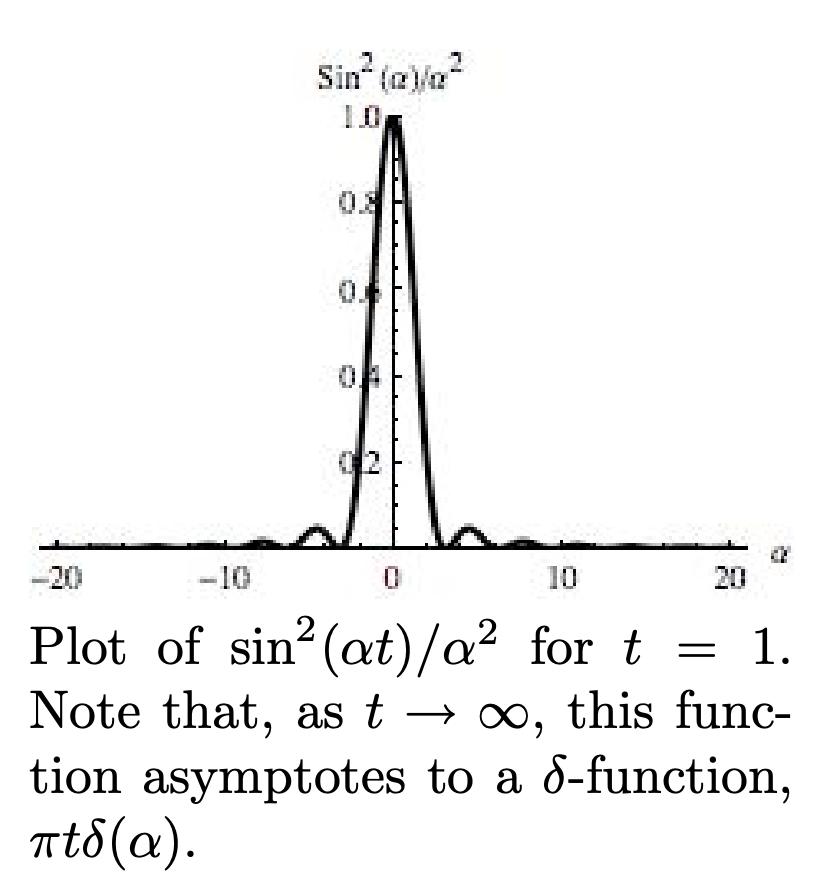
\[P_{i \to f}(t) = \frac{1}{\hbar^2} \left| \bra{f} V \ket{i} \right|^2 \frac{\sin^2(\alpha t)}{\alpha^2}\]

As $t$ approaches infinity, the function asymptotes to a delta function $\pi t \delta(\alpha)$ as shown in figure below, indicating that the likelihood of transition is proportional to the time elapsed. To obtain the transition rate, we divide by $t$:

\[\boxed{ R_{i \to f}(t) = \lim_{t \to \infty} \frac{P_{i \to f}(t)}{t} = \frac{2\pi}{\hbar^2} \left| \bra{f} V \ket{i} \right|^2 \delta(\omega_{fi} - \omega)}\]

This result is known as Fermi’s Golden Rule. Although named after Enrico Fermi, much of the foundational work was done by P.A.M. Dirac in an earlier study, who formulated a nearly identical equation involving a constant, the matrix element of the perturbation, and an energy difference.