Stark Effect in Hydrogen Atom

In the hydrogen atom, the energy levels are determined by the principal quantum number $n$, and for a given $n$, the energy is given by:

\[E_n^{(0)} = -\frac{13.6 \, \text{eV}}{n^2}\]

For $n = 2$, the energy level is:

\[E_2^{(0)} = -\frac{13.6 \, \text{eV}}{4} = -3.4 \, \text{eV}\]

This level is four-fold degenerate because there are multiple quantum states with the same energy. The states are specified by the quantum numbers $n$, $l$, and $m_l$, where:

$n$ is the principal quantum number,
$l$ is the orbital angular momentum quantum number, which can take values from $0$ to $n-1$,
$m_l$ is the magnetic quantum number, which can take values from $-l$ to $l$.

For $n = 2.$ $l$ can be $0$ (s-orbital) or $1$ (p-orbital):

For $l = 0$, $m_l = 0$.
For $l = 1$, $m_l = -1, 0, 1$.

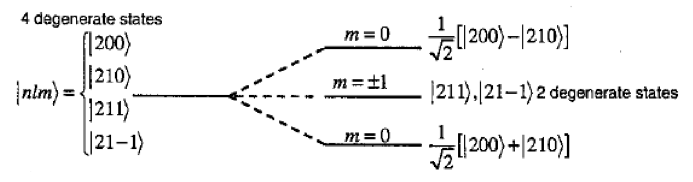
Thus, the ( n = 2 ) level has the following four degenerate states:

$ \ket{2,0,0}$ (2s state)
$ \ket{2,1,0}$ (2p state)
$ \ket{2,1,1}$ (2p state)
$ \ket{2,1,-1}$ (2p state)

These states are degenerate in the absence of an external electric field. In presence of electric field they split as shown in figure given below:

degenerate

Perturbation: The Stark Effect

When an external electric field $\mathcal{E}$ is applied along the $z$-axis, the Hamiltonian is perturbed:

\[H = H_0 + \lambda H'\]

where $H_0$ is the unperturbed Hamiltonian, $\lambda$ is a small parameter, and $H'$ is the perturbation due to the electric field. The perturbation Hamiltonian $H'$ is:

\[H' = e\mathcal{E}z\]

In spherical coordinates, $z = r\cos\theta$, so:

\[H' = e\mathcal{E}r\cos\theta\]

The task is to find the first-order corrections to the energy levels and eigenfunctions due to this perturbation.

Matrix Elements of the Perturbation

To find the corrections, we need to calculate the matrix elements of $H'$ in the subspace of the degenerate states. The degenerate states for $n = 2$ are:

\[\psi_{200}^{(0)}, \, \psi_{211}^{(0)}, \, \psi_{210}^{(0)}, \, \psi_{21-1}^{(0)}\]

where:

$\psi_{200}^{(0)}$ is the 2s state.
$\psi_{211}^{(0)}$, $\psi_{210}^{(0)}$, $\psi_{21-1}^{(0)}$ are the 2p states.

The matrix elements $H’_{ij} = \brakett{\psi_i^{(0)}}{H’}{\psi_j^{(0)}}$ are:

\[H'_{11} = \brakett{\psi_{200}^{(0)}}{e\mathcal{E}z}{\psi_{200}^{(0)}} = 0\;\text{(due to parity)}\]
\[H'_{12} = \brakett{\psi_{200}^{(0)}}{e\mathcal{E}z}{\psi_{211}^{(0)}}\]
\[H'_{13} = \brakett{\psi_{200}^{(0)}}{e\mathcal{E}z}{\psi_{210}^{(0)}}\]
\[H'_{14} = \brakett{\psi_{200}^{(0)}}{e\mathcal{E}z}{\psi_{21-1}^{(0)}}\]
\[H'_{22} = \brakett{\psi_{211}^{(0)}}{e\mathcal{E}z}{\psi_{211}^{(0)}}\]
\[H'_{33} = \brakett{\psi_{210}^{(0)}}{e\mathcal{E}z}{\psi_{210}^{(0)}}\]
\[H'_{44} = \brakett{\psi_{21-1}^{(0)}}{e\mathcal{E}z}{\psi_{21-1}^{(0)}}\]

These elements need to be calculated. For simplicity, we consider the known spherical harmonics and radial functions.

Calculating Matrix Elements

The matrix elements for the 2s and 2p states involve the radial part $R_{nl}$ and the angular part $Y_{lm}$.

For $n = 2$:

Radial Part:
- $R_{20}(r)$ for 2s state
- $R_{21}(r)$ for 2p states
Angular Part:
- $Y_{00}$ for $l = 0, m = 0$
- $Y_{1m}$ for $l = 1, m = -1, 0, 1$

For the Stark effect, the relevant spherical harmonics are:

\[Y_1^0 = \sqrt{\frac{3}{4\pi}} \cos\theta\] \[Y_1^{\pm1} = \mp\sqrt{\frac{3}{8\pi}} \sin\theta e^{\pm i\phi}\]

Non-Zero Matrix Elements

Using these, we find the non-zero matrix elements:

\[H'_{13} = \langle \psi_{200}^{(0)} | e\mathcal{E}z | \psi_{210}^{(0)} \rangle = e\mathcal{E} \langle 200 | r\cos\theta | 210 \rangle\]

The radial part can be computed as:

\[\int_0^\infty r^3 R_{20} R_{21} \, dr\]

And the angular part:

\[\int Y_{00} \cos\theta Y_{10} \, d\Omega\]

Combining these gives:

\[H'_{13} = e\mathcal{E} \left( \frac{3a_0}{2\sqrt{2}} \right) \sqrt{\frac{3}{4\pi}} \int_0^\infty r^3 R_{20} R_{21} \, dr\]

Solving the Secular Equation

We construct the perturbation matrix $H'$ in the subspace of the $n = 2$ states and solve the secular equation:

\[\begin{vmatrix} H'_{11} - E^{(1)} & H'_{12} & H'_{13} & H'_{14} \\ H'_{21} & H'_{22} - E^{(1)} & H'_{23} & H'_{24} \\ H'_{31} & H'_{32} & H'_{33} - E^{(1)} & H'_{34} \\ H'_{41} & H'_{42} & H'_{43} & H'_{44} - E^{(1)} \end{vmatrix} = 0\]

Since only $H'_{13}=\;H'_{31}=-3e \mathcal{E} a_0$ term is non-zero therefore we have

\[\begin{vmatrix} - E^{(1)} & 0 & -3e \mathcal{E} a_0 & 0 \\ 0 & - E^{(1)} & 0 & 0 \\ -3e \mathcal{E} a_0 & 0 & - E^{(1)} & 0 \\ 0 & 0 & 0 & - E^{(1)} \end{vmatrix} = 0\]

where $a_0$ is the Bohr radius. Given the symmetry and properties of the hydrogen atom, we find that the first-order energy corrections $E_{2,m}^{(1)}$ are:

\[E_{2,m}^{(1)} = \pm 3e \mathcal{E} a_0\]

Conclusion

An external electric field lifts the degeneracy of the $n = 2$ level in the hydrogen atom, splitting it into distinct energy levels.

Additional Material

In the hydrogen atom, the radial wave functions $R_{nl}(r)$ are solutions to the radial part of the Schrödinger equation. For the hydrogen atom, the radial wave functions are given by:

\[R_{nl}(r) = \sqrt{\frac{(n-l-1)!}{2n(n+l)!}} \left(\frac{2r}{na_0}\right)^l e^{-r/na_0} L_{n-l-1}^{2l+1} \left(\frac{2r}{na_0}\right)\]

where $L_{n-l-1}^{2l+1}$ are the associated Laguerre polynomials, $a_0$ is the Bohr radius, and $n$ and $l$ are the principal and orbital angular momentum quantum numbers, respectively.

Radial Wave Functions for $n = 2$

For $n = 2$, $l = 0$ (2s state):

\[R_{20}(r) = \sqrt{\frac{1}{4a_0^3}} \left(1 - \frac{r}{2a_0}\right) e^{-r/2a_0}\]

Here, $L_{1}^{1} \left(\frac{2r}{2a_0}\right) = 1 - \frac{r}{2a_0}$

For $n = 2$, $l = 1$ (2p state):

\[R_{21}(r) = \sqrt{\frac{1}{24a_0^3}} \left(\frac{r}{a_0}\right) e^{-r/2a_0}\]

Here, $L_{1}^{3} \left(\frac{2r}{2a_0}\right) = \frac{r}{a_0}$