Rate Equations for a Three-Level Laser System

A three-level laser system operates using the principle of stimulated emission of radiation. The rate equations describe how the populations of various energy levels change under the influence of pumping and laser radiation. The goal is to achieve population inversion, which is necessary for laser action.

The Three-Level System

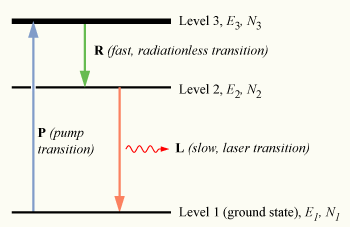
In a three-level laser system, atoms or molecules transition between three distinct energy levels:

1. Ground State (Level 1, $E_1$): The initial state with the population $N_1$.
2. Excited State (Level 3, $E_3$): The state to which atoms are pumped from the ground state, with the population $N_3$.
3. Metastable State (Level 2, $E_2$): A relatively stable excited state where population inversion occurs, with the population $N_2$.

• Pumping Transition (1 → 3): Atoms are pumped from the ground state (1) to the excited state (3).
• Lasing Transition (2 → 1): Atoms transition from the metastable state (2) to the ground state (1), emitting laser radiation.
• Rapid Decay (3 → 2): Atoms in state (3) quickly decay to state (2) through nonradiative processes.

Rate Equations

Let $N_1$, $N_2$, and $N_3$ be the populations of levels 1, 2, and 3, respectively. The total number of atoms per unit volume is:

$ N = N_1 + N_2 + N_3 $

1. Population Rate of Level 3 (Excited State):

$ \frac{dN_3}{dt} = W_p (N_1 - N_3) - N_3 T_{32} $

• $W_p N_1$ represents the rate of induced absorption for the 1 → 3 transition.
• $W_p N_3$ represents the rate of stimulated emission for the 3 → 1 transition.
• $T_{32} = A_{32} + S_{32}$ is the total relaxation rate from level 3 to level 2, where:
  • $A_{32}$ is the Einstein A coefficient for spontaneous emission.
  • $S_{32}$ is the nonradiative transition rate.

1. Population Rate of Level 2 (Metastable State):

$ \frac{dN_2}{dt} = W_l (N_1 - N_2) + N_3 T_{32} - N_2 T_{21} $

• $W_l (N_1 - N_2)$ represents the stimulated transitions between levels 1 and 2 (2 → 1 lasing).
• $N_3 T_{32}$ represents the spontaneous transitions from level 3 to level 2.
• $N_2 T_{21}$ represents the spontaneous transitions from level 2 to level 1.
• $W_l$ is proportional to the Einstein B coefficient $B_{21}$ and the energy density of the lasing transition.
• $T_{21} \approx A_{21}$ represents the spontaneous relaxation rate from level 2 to level 1.

1. Population Rate of Level 1 (Ground State):

$ \frac{dN_1}{dt} = W_p (N_3 - N_1) + W_l (N_2 - N_1) + N_2 T_{21} $

• $W_p (N_3 - N_1)$ represents the net stimulated transitions between levels 1 and 3.
• $W_l (N_2 - N_1)$ represents the stimulated transitions between levels 1 and 2.
• $N_2 T_{21}$ represents the spontaneous transitions from level 2 to level 1.

1. Conservation of Population:

$ \frac{dN_1}{dt} + \frac{dN_2}{dt} + \frac{dN_3}{dt} = 0 $

Equations (2), (4), and (5) are referred to as the rate equations for a three-level laser system.

Steady-State Solutions

At steady state, the time derivatives of the populations are zero:

$ \frac{dN_1}{dt} = 0, \quad \frac{dN_2}{dt} = 0, \quad \frac{dN_3}{dt} = 0 $

1. For Level 3:

$ N_3 = \frac{W_p}{W_p + T_{32}} N_1 $

1. For Level 2:

$ N_2 = \frac{W_l + \frac{T_{32} W_p}{W_p + T_{32}}}{W_l + T_{21}} N_1 $

1. Population Difference Between Levels 2 and 1:

$ \frac{N_2 - N_1}{N} = \frac{W_p (T_{32} - T_{21}) - T_{32} T_{21}}{3W_p W_l + 2W_p T_{21} + 2T_{32} W_l + T_{32} W_p + T_{32} T_{21}} $

Condition for Population Inversion

To achieve population inversion between levels 2 and 1 ($N_2 > N_1$), a necessary condition is:

$ T_{32} > T_{21} $

• The relaxation rate from level 3 to level 2 must be greater than that from level 2 to level 1.
• The lifetime of level 3 must be shorter than that of level 2.

Minimum Pumping Rate for Population Inversion

A minimum pumping rate $W_p$ is required to maintain population inversion:

$ W_{p,\text{min}} = \frac{T_{32} T_{21}}{T_{32} - T_{21}} $

For population inversion to occur, the actual pumping rate $W_p$ must be greater than $W_{p,\text{min}}$.