Rajesh Kumar

Plasma Oscillations and Plasmons

by Rajesh Kumar 3 min read

Learning Objectives:

  • Understand what plasma oscillations are and how they arise.
  • Define plasmons and relate them to quantized plasma oscillations.
  • Derive the plasma frequency and appreciate its physical significance.

Key Concepts / Definitions

  • Plasma: A quasi-neutral gas of charged and neutral particles which exhibits collective behavior.
  • Plasma Oscillation: A coherent oscillation of the electron density in a conducting medium relative to the positive ion background.
  • Plasmon: A quantum of plasma oscillation, representing the collective excitation of free electron gas.

Theory and Explanation

Plasma is often referred to as the “fourth state of matter” where electrons are not bound to atoms, and instead, they form a gas of free-moving charges. When these electrons are disturbed from their equilibrium position, they experience a restoring electrostatic force due to separation from the positively charged ion background. This leads to collective oscillations known as plasma oscillations.

Derivation of Plasma Frequency

Consider a uniform background of positive ions with number density $n_0$, and electrons of the same density but mobile. Assume electrons are displaced slightly by a distance $x$ from their equilibrium position. This creates an electric field due to charge separation.

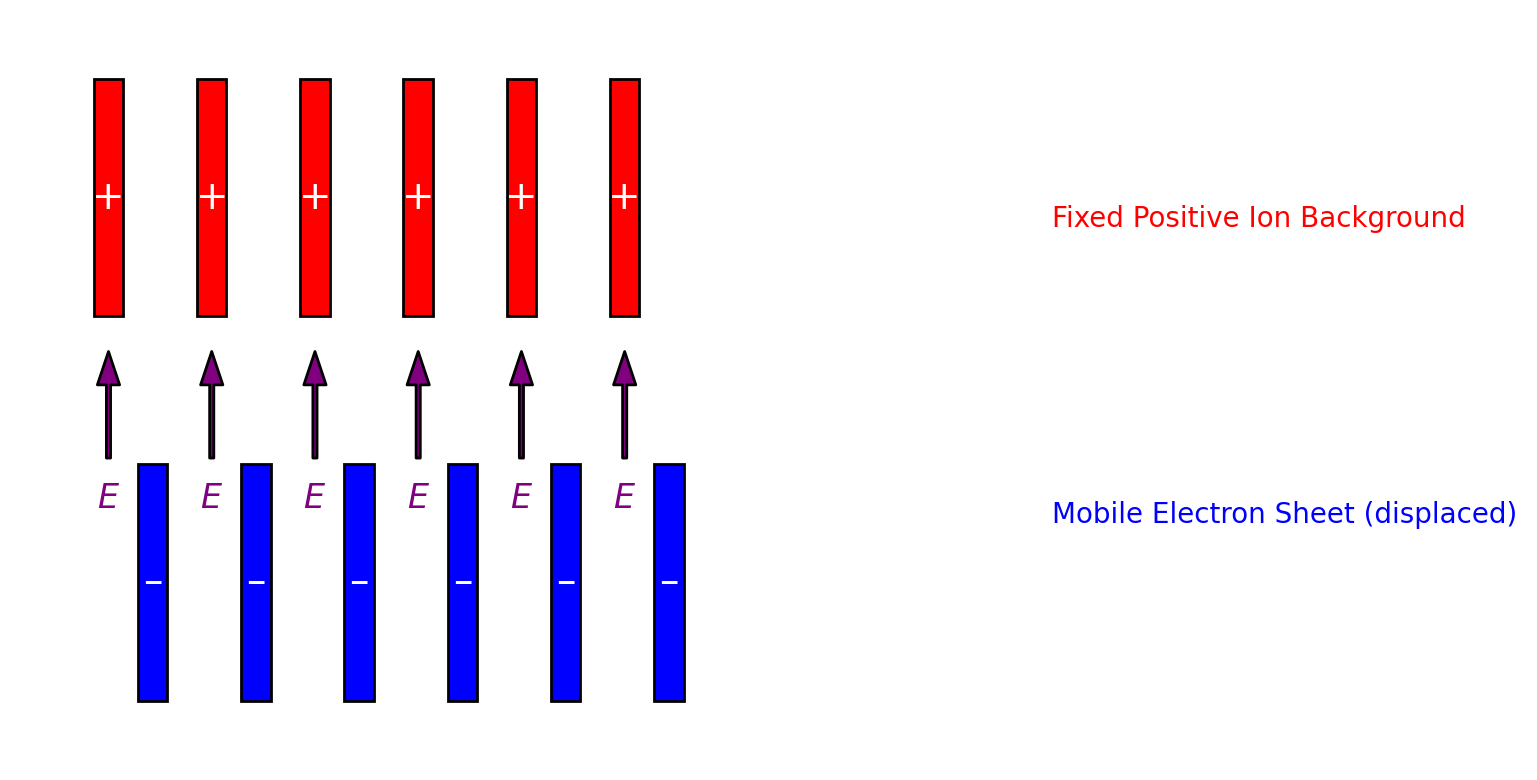
Interaction Process

Let $-e$ be the charge of an electron and $m$ be its mass. The displaced electron sheet creates a restoring electric field $E$ given by:

\[E = \frac{n_0 e x}{\varepsilon_0}\]

The force on an electron is then:

\[F = -e E = -\frac{n_0 e^2 x}{\varepsilon_0}\]

Using Newton’s second law:

\[m \frac{d^2 x}{dt^2} = -\frac{n_0 e^2 x}{\varepsilon_0}\]

This is the equation of simple harmonic motion with angular frequency $\omega_p$:

\[\omega_p^2 = \frac{n_0 e^2}{\varepsilon_0 m}\]

Therefore, the plasma frequency is:

\[\omega_p = \sqrt{\frac{n_0 e^2}{\varepsilon_0 m}}\]

This is the natural frequency at which the electron gas oscillates around its equilibrium position in the plasma.

Plasmons

Plasmons are the quantum mechanical counterpart of plasma oscillations. Just as photons are quanta of electromagnetic waves, plasmons are quanta of these collective oscillations.

In quantum theory, the energy associated with a plasmon is:

\[E = \hbar \omega_p\]

Plasmons play a key role in the optical properties of metals and are used in fields like plasmonics and nanophotonics.

Solved Examples

  • Example 1:
    Problem: Calculate the plasma frequency of electrons in a metal with electron density $n_0 = 8.5 \times 10^{28} \ \text{electrons/m}^3$.
    Solution:
    Using the formula:
    \(\omega_p = \sqrt{\frac{n_0 e^2}{\varepsilon_0 m}}\)
    Plugging in values:
    $n_0 = 8.5 \times 10^{28}$
    $e = 1.6 \times 10^{-19} \ \text{C}$
    $\varepsilon_0 = 8.85 \times 10^{-12} \ \text{F/m}$
    $m = 9.11 \times 10^{-31} \ \text{kg}$

    \[\omega_p = \sqrt{\frac{(8.5 \times 10^{28})(1.6 \times 10^{-19})^2}{(8.85 \times 10^{-12})(9.11 \times 10^{-31})}} \approx 1.64 \times 10^{16} \ \text{rad/s}\]

  • Example 2:
    Problem: What is the energy of a plasmon with plasma frequency $\omega_p = 1.5 \times 10^{16} \ \text{rad/s}$?
    Solution:
    \(E = \hbar \omega_p\)
    $\hbar = 1.055 \times 10^{-34} \ \text{J·s}$
    \(E = (1.055 \times 10^{-34}) (1.5 \times 10^{16}) = 1.58 \times 10^{-18} \ \text{J}\)
    In eV:
    \(E = \frac{1.58 \times 10^{-18}}{1.6 \times 10^{-19}} \approx 9.87 \ \text{eV}\)

Important Points / Summary

  • Plasma oscillations are collective movements of electron density in a plasma.
  • The plasma frequency depends only on the electron density and is independent of the wavevector.
  • Plasmons are quantized plasma oscillations and are important in understanding optical and electronic properties of materials.

Practice Questions

Short Answer:

  1. What is plasma and how is it different from a neutral gas?
  2. Define the term “plasma frequency” and explain its physical significance.

Numerical:

  1. Calculate the plasma frequency of a semiconductor with electron density $n = 10^{21} \ \text{m}^{-3}$.
  2. What is the plasmon energy in a metal with $\omega_p = 2.0 \times 10^{16} \ \text{rad/s}$?

MCQs:

  1. The plasma frequency $\omega_p$:
    • (a) increases with increasing mass of electrons
    • (b) decreases with increasing electron density
    • (c) increases with increasing electron density
    • (d) is independent of electron density
      Answer: (c)
  2. Plasmons are:
    • (a) individual electrons
    • (b) phonons in a crystal lattice
    • (c) quantum of electromagnetic waves
    • (d) quanta of plasma oscillations
      Answer: (d)