Polarons
In solid-state physics, polarons are quasiparticles formed due to the interaction of an electron (or hole) with the phonons (quantized lattice vibrations) in an ionic crystal. This interaction leads to a modification of the electron’s motion, as it becomes “dressed” with a polarization cloud of lattice distortion.
A key observable effect of electron-phonon interaction is the temperature dependence of electrical resistivity. As temperature increases:
- The number of phonons increases.
- This leads to more scattering of electrons, which increases the resistivity.
Example: In pure copper,
- At 0 °C, resistivity ≈ 1.55 μΩ·cm
- At 100 °C, resistivity ≈ 2.28 μΩ·cm
Above the Debye temperature (θD ≈ 70 °C for Cu), the phonon population becomes roughly proportional to the absolute temperature (T), so:
\[\rho(T) \propto T\]Vibrational Modes in Ionic Crystals
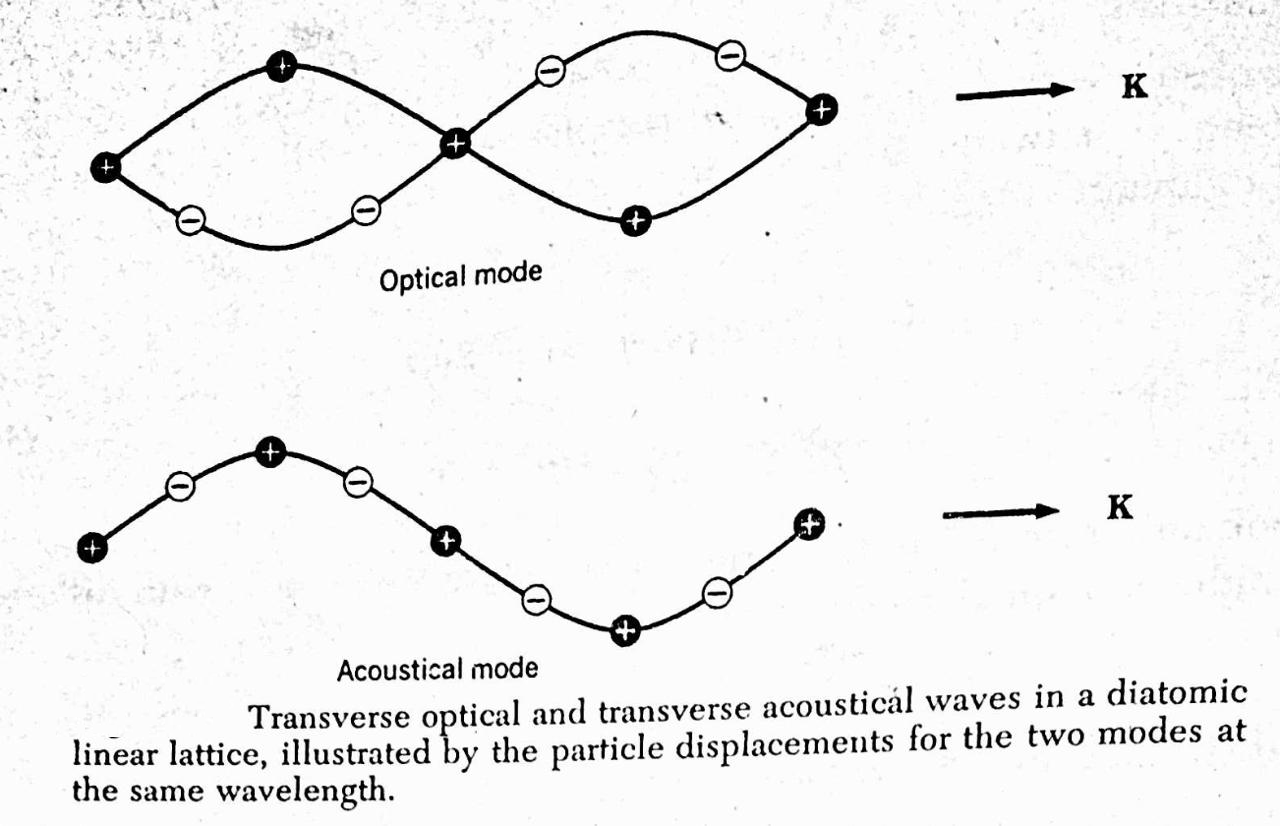
In a crystal, atoms vibrate about their equilibrium positions, leading to the formation of phonon branches:
- Acoustic Modes: Low-energy vibrations where atoms move in phase.
- Optical Modes: Higher-energy modes where adjacent atoms in the basis move out of phase.
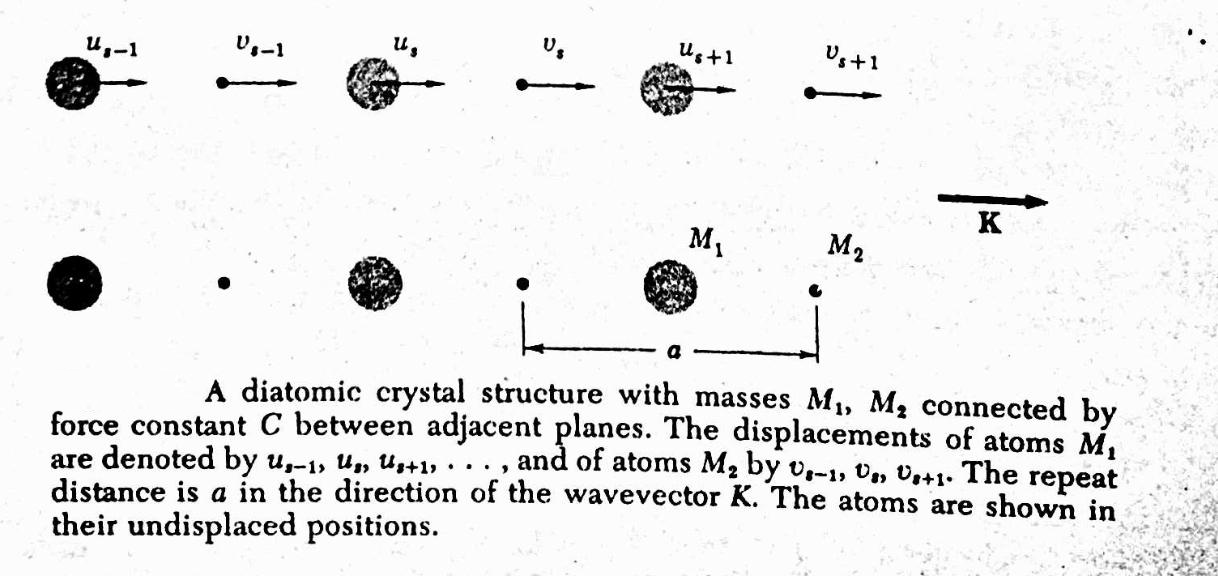
Assuming nearest-neighbor interactions and identical force constants $ C $, we get:
\[M_1 \ddot{u}_n = C (v_{n} + v_{n-1} - 2 u_n)\] \[M_2 \ddot{v}_n = C (u_{n+1} + u_n - 2 v_n)\]We assume traveling wave solutions:
\[u_n = u\, e^{i(kna - \omega t)}, \quad v_n = v\, e^{i(kna - \omega t)}\]Substituting these into the equations yields a system of homogeneous linear equations for $ u $ and $ v $, leading to the dispersion relation.
The frequency solutions $ \omega(k) $ show two branches:
Acoustic Branch
\[\omega^2 \approx \frac{\frac{1}{2}C a^2 k^2}{M_1 + M_2} \quad \text{(for small $ k $)}\]- Both atoms move in phase.
- Represents long-wavelength sound waves.
Optical Branch
\[\omega^2 \approx \frac{2C}{M_1 M_2}(M_1 + M_2)\]- Atoms move out of phase.
- Can be excited by electromagnetic radiation (especially when atoms are oppositely charged).
At zone boundary $ K_{\text{max}} = \pi/a $:
\[\omega_1^2 = \frac{2C}{M_1}, \quad \omega_2^2 = \frac{2C}{M_2}\]This gives rise to a frequency gap in the phonon spectrum.