3D Collision
The theory of collision in three dimensions is a fundamental aspect of quantum scattering, describing how a particle interacts with a potential when motion is not restricted to a single line but occurs in full three-dimensional space. Unlike one-dimensional scattering, where the particle approaches the potential from the left or right, three-dimensional collisions require the description of wave propagation in spherical geometry. This approach is crucial in understanding atomic, nuclear, and molecular processes where interactions occur isotropically.
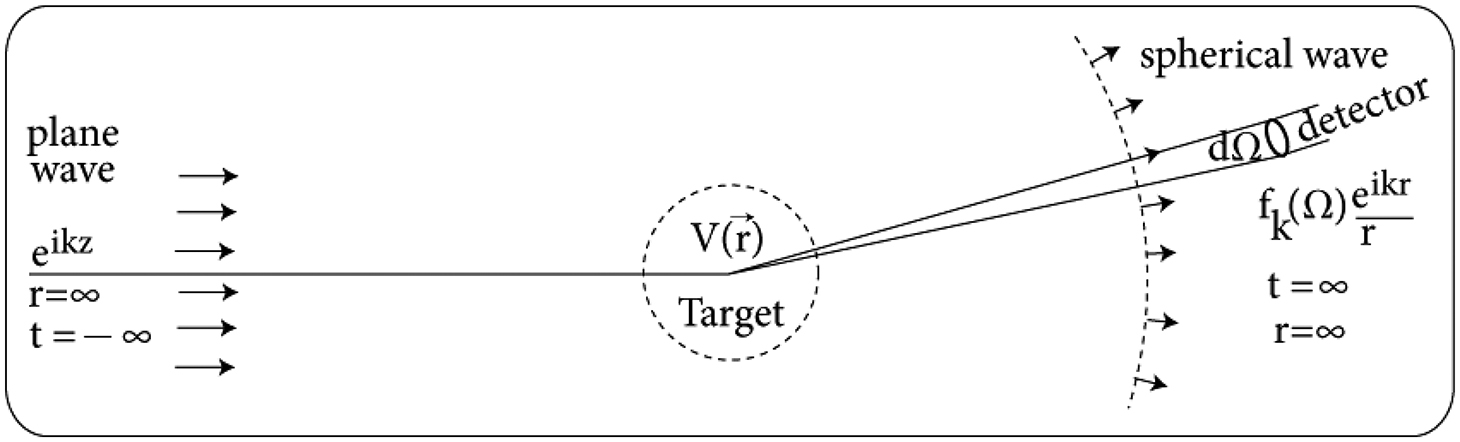
In three dimensions, a free particle is represented by a plane wave of the form
\(\psi_{\text{inc}} = e^{i\mathbf{k}\cdot\mathbf{r}},\)
where $ \mathbf{k} $ is the incident wave vector. When the particle encounters a scattering potential $ V(r) $, the scattered part of the wave appears as an outgoing spherical wave. The total wavefunction becomes
\(\psi(\mathbf{r}) = e^{i\mathbf{k}\cdot\mathbf{r}} + f(\theta,\phi)\frac{e^{ikr}}{r},\)
where $ f(\theta,\phi) $ is the scattering amplitude, fully encapsulating the angular distribution of the scattered particles.
The solution to the Schrödinger equation in three dimensions is typically expressed using spherical coordinates due to the central nature of most scattering potentials. The angular dependence is treated using spherical harmonics $ Y_{\ell m}(\theta,\phi) $, while the radial part is determined by solving a differential equation for each angular momentum quantum number $ \ell $. This leads to partial wave analysis, one of the most powerful methods in quantum scattering theory.
When a particle collides with a spherically symmetric potential, angular momentum is conserved, enabling decomposition of the incident wave into partial waves. Each partial wave experiences a phase shift $ \delta_\ell $ due to the potential. These phase shifts measure how much each wave is delayed or advanced relative to a free particle. The total scattering amplitude is obtained by summing contributions from all partial waves: \(f(\theta) = \sum_{\ell=0}^{\infty}(2\ell+1)\frac{e^{2i\delta_\ell}-1}{2ik}P_\ell(\cos\theta),\) where $ P_\ell(\cos\theta) $ are Legendre polynomials.
The measurable quantity in scattering, the differential cross-section, is given by
\(\frac{d\sigma}{d\Omega} = |f(\theta,\phi)|^2.\)
This describes how the intensity of scattered particles varies with direction. The total cross-section is obtained by integrating over all angles. Three-dimensional scattering theory is essential for interpreting low-energy nuclear collisions, electron-atom scattering, neutron scattering, and molecular collisions.
Supplementary Readings
Schrödinger Equation in 3D
For a particle with energy $ E = \frac{\hbar^2 k^2}{2m} $, the time-independent Schrödinger equation is:
\[\nabla^2\psi + k^2\psi = \frac{2m}{\hbar^2}V(r)\psi.\]Spherical Decomposition
Using spherical symmetry, \(\psi(r,\theta,\phi) = \sum_{\ell,m} R_\ell(r) Y_{\ell m}(\theta,\phi).\)
Radial Equation
The radial function satisfies: \(\frac{d^2u_\ell}{dr^2} + \left[k^2 - \frac{\ell(\ell+1)}{r^2} - \frac{2mV(r)}{\hbar^2}\right]u_\ell = 0,\) where $ u_\ell = rR_\ell $.
Asymptotic Form
For large $ r $, \(u_\ell(r) \sim \sin\left(kr - \frac{\ell\pi}{2} + \delta_\ell\right).\)
Scattering Amplitude
Using partial wave expansion: \(f(\theta) = \frac{1}{k} \sum_{\ell=0}^{\infty}(2\ell+1)e^{i\delta_\ell}\sin\delta_\ell\, P_\ell(\cos\theta).\)
Differential Cross-Section
\(\frac{d\sigma}{d\Omega} = |f(\theta)|^2.\)
Total Cross-Section
\(\sigma_{\text{tot}} = \frac{4\pi}{k^2} \sum_{\ell=0}^{\infty}(2\ell+1)\sin^2\delta_\ell.\)