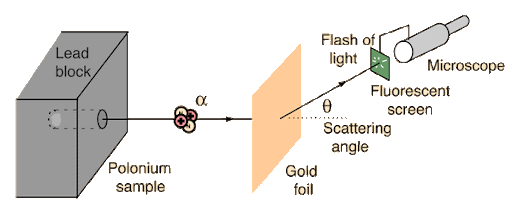
Alpha Scattering
Alpha (α) scattering refers to the interaction of alpha particles—helium nuclei consisting of two protons and two neutrons—with atomic nuclei or atoms. The study of α-scattering has played one of the most pivotal roles in the development of modern physics. Historically, Rutherford’s α-scattering experiments in 1909 led to the discovery of the atomic nucleus and gave rise to the planetary model of the atom. These experiments showed that most α-particles pass through thin metal foils with little deflection, while a very small fraction undergo large-angle scattering, revealing the presence of a compact and massive nucleus.
In quantum scattering theory, α-particles interacting with atomic nuclei are treated through the Coulomb potential, since both projectile and target carry positive charge. The long-range nature of the Coulomb field makes α-scattering distinct from short-range nuclear scattering. Classical mechanics provides a useful description in terms of trajectories, impact parameters, and scattering angles, but a complete interpretation requires quantum mechanics, especially at low energies or when nuclear forces become relevant.
The Coulomb interaction between an α-particle of charge $ +2e $ and a nucleus of charge $ +Ze $ is given by:
\[V(r) = \frac{2Ze^2}{4\pi\epsilon_0 r}.\]This central potential leads to hyperbolic trajectories, where the deflection angle depends on the impact parameter. Rutherford derived the differential cross-section in classical terms and predicted an angular distribution:
\[\frac{d\sigma}{d\Omega} \propto \frac{1}{\sin^4(\theta/2)}.\]This formula matched experimental data exceptionally well for large impact parameters (i.e., small scattering angles), demonstrating that the Coulomb potential dominates the interaction.
Quantum mechanically, α-scattering is treated using partial waves, similar to other scattering processes. The phase shifts are determined by comparing the asymptotic form of the wavefunction with Coulomb-modified spherical waves. The scattering amplitude is influenced by both the long-range Coulomb field and, if the α-particle approaches close enough, the short-range nuclear potential. This leads to resonances, enhanced cross-sections, and deviations from the simple Rutherford formula at small distances. Such quantum effects have been crucial in understanding nuclear sizes, nuclear charge distributions, and the onset of nuclear forces.
Supplementary Readings
Coulomb Potential
The α-particle experiences the potential: \(V(r) = \frac{2Ze^2}{4\pi\epsilon_0 r}.\)
Classical Scattering
Using impact parameter $ b $ and scattering angle $ \theta $,
\(\cot\left(\frac{\theta}{2}\right) = \frac{2bE}{k},\)
where
\(k = \frac{2Ze^2}{4\pi\epsilon_0}.\)
Rutherford Differential Cross-Section
Expressing cross-section in terms of impact parameter: \(\frac{d\sigma}{d\Omega} = \left(\frac{k}{4E}\right)^2 \frac{1}{\sin^4(\theta/2)}.\)
Quantum Mechanical Scattering
The wavefunction in presence of Coulomb potential behaves as: \(\psi(r,\theta) \sim e^{i\mathbf{k\cdot r}} + f_C(\theta)\frac{e^{ikr}}{r}.\)
The Coulomb scattering amplitude: \(f_C(\theta) = -\frac{\eta}{2k\sin^2(\theta/2)} e^{-2i\eta \ln[\sin(\theta/2)]},\) with Sommerfeld parameter: \(\eta = \frac{Z_1 Z_2 e^2}{4\pi\epsilon_0\hbar v}.\)
Quantum deviations from Rutherford formula appear when nuclear forces influence scattering, often at large angles.